|
|
Кривые Безье.
Содержание статьи:
Введение.
Алгоритмическая база.
Реализация.
Введение.
к началу статьи
Приветствую всех! Сейчас 2:17 ночи, через 3 часа мне нужно будет сорваться с места и бежать на работу, что бы хотя бы в этот раз сдать релиз вовремя. Нашей службе это никогда прежде не удавалось... Но в этот раз, я уверен, нам повезет! Не только этот день, а вообще последние несколько недель выдались чересчур жаркими даже для меня: абсолютно нереальный государственный экзамен за все 4 года учебы, шлифовка бакалавра с последующей блестящей защитой, опять-таки релиз.... Все свободное время занимал сон (пять или шесть часов, не больше), но сегодня я решил от него отказаться ради того, что бы продемонстрировать Вам как работать с кубическими кривыми Безье. Если по каким-то причинам Вы о них никогда не слыхали, не отчаивайтесь – я постарался сделать статью максимально доступной. За сим считаю лирическое отступление законченным. Можно кодить?
Алгоритмическая база.
к началу статьи
Кривая Безье задается несколькими точками в N-мерном пространстве (классический вариант, описываемый в литературе – 4 точки, но мы, для удобства, помимо этого случая будем использовать вырожденные случаи из 3-х точек, а так же пользоваться введением дополнительных вершин), но нам так много не нужно, поэтому ограничимся тремя измерениями (хотя все приведенные алгоритмы будут справедливы и для векторов другой мерности).
Для начала рассмотрим самый простой случай (его иллюстрация этого случая приведена на рис. 1) – когда у нас 4 вершины.
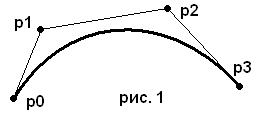
Здесь p0 и p3 – начальная и конечная точки соответственно, а p1 и p2 – промежуточные точки. Разности же вершин p1-p0 и p2-p3 определяют крутизну кривой в этих точках. Сама же кривая задается следующим уравнением:
|
C(s) = p0 * ( 1 – s ) ^ 3 + 3 * p1 * s * ( 1 – s )^2 + 3 * p2 * s ^ 2 * ( 1 – s ) + p3 * s ^ 3
| |
Несложно показать, что
|
C( 0 ) = p0
C( 1 ) = p3
C’( 0 ) = 3 * ( p1 - p0 )
C’( 1 ) = 3 * ( p3 – p2 )
| |
Собственно как я и говорил – кривая проходит через конечные точки + имеется информация о крутизне кривой.
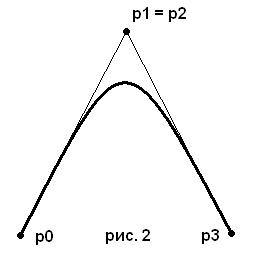
Но можно построить кривую Безье и по трем точкам. В этом случае p1 и p2 будут одинаковые. Правда в этом случае мы лишимся возможности перекручивать нашу кривую, плюс сама кривая будет не такая гладкая, как если бы она строилась по четырём точкам (рис. 2).
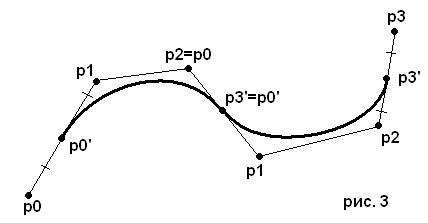
Наверняка с кривыми из 4 вершин Вы быстро наиграетесь и захотите задавать более длинные и изощренные кривые с петлями, изломами… Из 4 точек их уже не составить, поэтому придется стыковать их. Но как это осуществить? Если мя просто сделаем так, что бы последняя вершина первой кривой совпадала с первой вершиной второй кривой, то мы получим излом. Это связано с тем, что производная меняется скачком – при подходе к концу кривой она у нас выгнута в одну сторону, а при проходе точки стыка она у нас мгновенно выгибается в другую сторону. Что бы этого не произошло, нам придется контролировать производную в точках стыка кусков кривых Безье. Вручную это делать как-то тоскливо, а автоматически не получиться, поэтому придется исхитриться. Собственно ничего сложного мы делать не будем – все детали Вы можете увидеть на рис. 3.
Реализация.
к началу статьи
По доброй (я надеюсь) традиции сначала рассмотрим класс:
|
#define BC_LOOPED 1
#define BC_TRI_VERTEX_CURVE 2
#define BC_QUAD_VERTEX_CURVE 4
#define BC_ABSOLUTE_LENGTH 8
#define BC_RELATIVE_LENGTH 16
class cBesierCurve{
cArray<cVector4> *Vertexes;
cArray<float> *SubCurveLengths;
int MODE;
float GetLength( cVector4 , cVector4 , cVector4 , cVector4 );
public:
float Length;
cBesierCurve( void ){Length = -1;Vertexes=NULL;SubCurveLengths=NULL;}
cVector4 operator()( float );
cVector4 operator()( float , cVector4 , cVector4 , cVector4 , cVector4 );
void AddVertex( cVector4 );
void SetMode( int _m ){MODE = _m;}
float GetLength( void );
void Render( cD3DDevice & , float );
void RenderCurveStructure( cD3DDevice & );
};
| |
Хочу обратить Ваше внимание на флаги в самом начале листинга, их значение следующее:
BC_LOOPED – из множества точек, хранящихся в массиве Vertexes будет создана составная зацикленная кривая Безье.
BC_TRI_VERTEX_CURVE – куски кривых Безье будут строится по 3 точкам (рис. 2)
BC_QUAD_VERTEX_CURVE – куски кривых Безье будут строится по 4точкам (рис. 1)
BC_ABSOLUTE_LENGTH и BC_RELATIVE_LENGTH – длина кривой будет измеряться в абсолютных или относительных величинах соответственно.
Создание нашей кривой начинается с определения точек, из которых она состоит:
|
void cBesierCurve::AddVertex( cVector4 v ){
if( !Vertexes ){
Vertexes = new cArray<cVector4>;
}
Vertexes->AddEnd( v );
}
| |
После чего устанавливаем тип кривой – SetMode( int _m ).
Затем осуществляем препроцессинг нашей кривой (рассмотрим здесь только часть функции) –
|
//минимальные проверки
if( !Vertexes ){
MessageBox( 0 , "В кривой нет вершин." , "Ошибка" , 0 );
exit( 0 );
}
if( !SubCurveLengths ){
SubCurveLengths = new cArray<float>;
}
//смотрим что за кривая
if( ( MODE & BC_QUAD_VERTEX_CURVE ) && ( MODE & BC_LOOPED ) ){
| |
Здесь мы проверяем что в зацикленной кривой, строящейся по 4 точкам, достаточно точек. Для данной кривой должно выполняться следующее условие - ( Vertexes->Cursor - 2 ) % 4. Для кривых другого типа это условие проще.
|
if( ( Vertexes->Cursor - 2 ) % 4 ){
MessageBox( 0 , "В кривой такого типа недостаточно вершин"
, "Ошибка" , 0 );
return( 0 );
}
| |
Наша кривая состоит из кусков кривых Безье. Для того что бы эффективно пользоваться этим классом вычислим длины этих частей заранее и сохраним их в массиве SubCurveLengths. Кстати длина куска Безье вычисляется функцией GetLength(cVector4 , cVector4 , cVector4 , cVector4 ).
|
Length = 0;
SubCurveLengths->SetLength( Vertexes->Cursor / 2 );
for( int i( 0 ) ; i < Vertexes->Cursor / 2 ; i++ ){
int i0( 2 * i + 0 - Vertexes->Cursor * ( ( 2 * i + 0 ) /
Vertexes->Cursor ) );
int i1( 2 * i + 1 - Vertexes->Cursor * ( ( 2 * i + 1 ) /
Vertexes->Cursor ) );
int i2( 2 * i + 2 - Vertexes->Cursor * ( ( 2 * i + 2 ) /
Vertexes->Cursor ) );
int i3( 2 * i + 3 - Vertexes->Cursor * ( ( 2 * i + 3 ) /
Vertexes->Cursor ) );
(*SubCurveLengths)[ i ] = GetLength(0.5 * ( (*Vertexes)[ i0 ] +
(*Vertexes)[ i1 ] ) , (*Vertexes)[ i1 ] ,
(*Vertexes)[ i2 ] , 0.5 * ( (*Vertexes)[ i3 ] +
(*Vertexes)[ i2 ] ) );
Length += (*SubCurveLengths)[ i ];
}
if( MODE & BC_RELATIVE_LENGTH ){
for( int i( 0 ) ; i < SubCurveLengths->Cursor ; i++ ){
(*SubCurveLengths)[ i ] /= Length;
}
Length = 1;
}
return( Length );
}
}
| |
Смысл же флагов BC_RELATIVE_LENGTH и BC_ABSOLUTE_LENGTH заключается в том, что в первом случае длина кривой будет из промежутка от 0 до 1, а во втором той длины, какая есть. На последок скажу, что функция GetLength(cVector4 , cVector4 , cVector4 , cVector4 ) длину кривой приблизительно, хотя и достаточно точно.
Все необходимы приготовления сделаны и можно наконец приступать к самому главному – параметризации нашей кривой:
|
cVector4 cBesierCurve::operator()( float t ){
float tmp( NULL );
int i( 0 );
float s;
if( ( MODE & BC_LOOPED ) ){
for( ; i < SubCurveLengths->Cursor && tmp +
(*SubCurveLengths)[ i ] < t ; i++ ){
tmp += (*SubCurveLengths)[ i ];
}
if( i == SubCurveLengths->Cursor )
s = ( ( t - tmp ) / (*SubCurveLengths)[ i - 1 ] );
else
s = ( ( t - tmp ) / (*SubCurveLengths)[ i ] );
}
else{
for( ; i < SubCurveLengths->Cursor - 1
&& tmp + (*SubCurveLengths)[ i ] < t ; i++ ){
tmp += (*SubCurveLengths)[ i ];
}
if( i == SubCurveLengths->Cursor )
s = ( ( t - tmp ) / (*SubCurveLengths)[ i - 1 ] );
else
s = ( ( t - tmp ) / (*SubCurveLengths)[ i ] );
}
if( MODE & BC_TRI_VERTEX_CURVE ){
int i0( i + 0 - Vertexes->Cursor * ( ( i + 0 ) / Vertexes->Cursor ) );
int i1( i + 1 - Vertexes->Cursor * ( ( i + 1 ) / Vertexes->Cursor ) );
int i2( i + 2 - Vertexes->Cursor * ( ( i + 2 ) / Vertexes->Cursor ) );
return( (*this)( s , 0.5 * ( (*Vertexes)[ i0 ] + (*Vertexes)[ i1 ] ) ,
(*Vertexes)[ i1 ] , (*Vertexes)[ i1 ] ,
0.5 * ( (*Vertexes)[ i2 ] + (*Vertexes)[ i1 ] )) );
}
if( MODE & BC_QUAD_VERTEX_CURVE ){
int i0( 2 * i + 0 - Vertexes->Cursor * ( ( 2 * i + 0 ) / Vertexes->Cursor ) );
int i1( 2 * i + 1 - Vertexes->Cursor * ( ( 2 * i + 1 ) / Vertexes->Cursor ) );
int i2( 2 * i + 2 - Vertexes->Cursor * ( ( 2 * i + 2 ) / Vertexes->Cursor ) );
int i3( 2 * i + 3 - Vertexes->Cursor * ( ( 2 * i + 3 ) / Vertexes->Cursor ) );
return( (*this)( s , 0.5 * ( (*Vertexes)[ i0 ] + (*Vertexes)[ i1 ] ) ,
(*Vertexes)[ i1 ] , (*Vertexes)[ i2 ] ,
0.5 * ( (*Vertexes)[ i2 ] + (*Vertexes)[ i3 ] )) );
}
MessageBox( 0 , "Неопознанный тип кривой (operator())." , "Ошибка" , 0 );
return( NULL );
}
| |
В этой функции мы сначала находим курсор i – первой вершины (p0) в куске Безье, а затем с помощью функции
|
cVector4 cBesierCurve::operator()( float t , cVector4 p0 ,
cVector4 p1 , cVector4 p2 , cVector4 p3 ){
return( ( 1 - t ) * ( 1 - t ) * ( 1 - t ) * p0 +
3 * t * ( 1 - t ) * ( 1 - t ) * p1 +
3 * t * t * ( 1 - t ) * p2 +
t * t * t * p3 );
}
| |
находим точку на кривой.
Вот пожалуй и все на сегодня. До встречи!
к началу статьи
Исходные коды.
|
|
|